Q&A thường gặp
Hãy xem qua những câu hỏi và câu trả lời thường gặp của hơn 100 triệu bạn bè Qanda và cùng học với họ!
21. Biết \(4^x + 4^{-x} = 23\) tính giá trị của biểu thức \(P = 2^x + 2^{-x}\)
A. 5
B. \(\sqrt{27}\)
C. \(\sqrt{23}\)
Đặt \(y = 2^x\), khi đó \(4^x = (2^x)^2 = y^2\) và \(4^{-x} = (2^{-x})^2 = \frac{1}{y^2}\). Suy ra:
\(
y^2 + \frac{1}{y^2} = 23.
\)
Nhận thấy:
\(
\bigl(y + \frac{1}{y}\bigr)^2 = y^2 + 2 + \frac{1}{y^2} = 23 + 2 = 25.
\)
Toán học

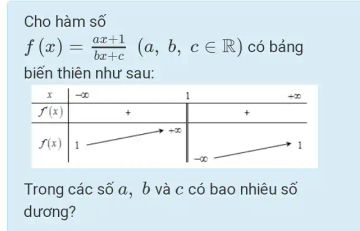
Cho hàm số
\(f(x) = \frac{ax+1}{bx+c}\) \((a, b, c \in \mathbb{R})\) có bảng
biến thiên như sau:
Trong các số \(a, b\) và \(c\) có bao nhiêu số
dương?
Step1. Thiết lập phương trình tiệm cận
Từ x = 1 là tiệm cận đứng, suy ra b(
Toán học
Câu 28. Trong không gian \(Oxyz\), cho mặt phẳng \((\alpha)\): \(ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P)\): \(x - y - z + 1 = 0\) và \((Q)\): \(x + 2y + z - 1 = 0\). Tính \(a + 4b\).
A. \(-16\).
B. \(-8\).
C. \(0\).
D. \(8\).
Step1. Tạo phương trình mặt phẳng (α) dưới dạng tổ hợp tuyến tính
Xét (α) =
Toán học

Cho \(cos2\alpha = \frac{2}{3}\). Tính giá trị của biểu thức \(P = cos\alpha.cos3\alpha\).
A. \(P = \frac{7}{18}\).
B. \(P = \frac{7}{9}\).
C. \(P = \frac{5}{9}\).
D. \(\frac{5}{18}\).
Step1. Tính cosα từ cos2α
Dùng công thức cos²α = (1 + cos2
Toán học

Câu 40: Cho hàm số \(y=f(x)\) có đạo hàm là \(f'(x)=ln(x+a), \forall x>-a\), a là số thực dương và \(f(0)=aln a\. Biết \(\int_{0}^{a}f(x)dx=0\), khi đó mệnh đề nào sau đây đúng?
A. \(a\in (2;e)\).
B. \(a\in (0;1)\).
C. \(a\in (1;\sqrt{2})\).
D. \(a\in (\frac{e}{2};2)\).
Step1. Tính tích phân ∫ln(x + a)dx
Đặt t = x +
Toán học

Câu 49. Cho hàm số bậc bốn \(y = f(x)\) có đồ thị hàm số \(y = f'(x)\) như hình vẽ. Số điểm cực trị của hàm số
\(h(x) = f(|3x - 2|) + 2022\) là
Step1. Xác định số nghiệm của f'(x) = 0
Dựa vào đồ thị f'
Toán học

1.8. Tính giá trị của các biểu thức sau:
a) \(\left(8+2\frac{1}{3}-\frac{3}{5}\right)-\left(5+0,4\right)-\left(3\frac{1}{3}-2\right)\);
b) \(\left(7-\frac{1}{2}-\frac{3}{4}\right):\left(5-\frac{1}{4}-\frac{5}{8}\right)\).
Step1. Chuyển đổi hỗn số trong biểu thứ
Toán học

Câu 58. Biểu thức \(A = \frac{{{{(1 - {{\tan }^2}x)}^2}}}{{4{{\tan }^2}x}} - \frac{1}{{4{{\sin }^2}x{{\cos }^2}x}}\) không phụ thuộc vào x và bằng
A. 1.
B. -1.
C. \(\frac{1}{4}\).
D. \( - \frac{1}{4}\).
Step1. Rút gọn (1 − tan² x)² / (4 tan² x)
Sử dụng đồng nhất thức
\(1 - \tan^2 x = \frac{\cos(2x)}{\cos^2 x}\)
Toán học

Bài 12: Gạch chân lỗi sai trong mỗi câu sau và sửa lại cho đúng:
1.Their life has been more comfortably since they moved to the city.
2.She looks more pretty in this white dress.
3.The manager wants us to work more hardly.
4.This week you looks more healthily than last week.
5.Everyone in my town is looking for more better crop this year.
6.Jim runs more fastly than his friends.
7.I think a settle life is more better than a nomadic life.
8.Today Jim performs less confident than usual.
9.The heavy rain makes it more difficultly to drive.
10.Their team preformed much more well than our team.
Step1. Xác định lỗi sai về dạng so sánh
Kiểm tra xem câu sử dụng t
Tiếng Anh

Câu 14. Cho dãy số \((u_n)\) là một cấp số cộng có \(u_1 = 3\) và công sai \(d = 4\). Biết tổng \(n\) số hạng đầu của dãy số \((u_n)\) là \(S_n = 253\). Tìm \(n\).
\(253 = S = \frac{n}{2}[2(3)+(n-1)4]\)
A. 9.
B. 11.
C. 12.
D. 10.
Ta có cấp số cộng với số hạng đầu \(u_1 = 3\) và công sai \(d = 4\). Tổng \(n\) số hạng đầu là:
\(\( S_n = \frac{n}{2}[2u_1 + (n-1)d]\)\)
Thay \(u_1 = 3\) và \(d = 4\) vào:
\(\( S_n = \frac{n}{2}[2\cdot 3 + (n-1)\cdot 4] = \frac{n}{2}(6 + 4n - 4) = \frac{n}{2}(4n + 2) = n(2n + 1).\)\)
Toán học

2.13. Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội cân có 9 học sinh. Hỏi có đội nào không có đủ 9 học sinh hay không?
2.14. Thay dấu * bởi một chữ số để số 345*:
Ta kiểm tra xem 162 có chia hết cho 9 hay không.
\(162 \div 9 = 18\)
Vì kết quả là 18,
Toán học
